#面试 #深度学习

卷积

反卷积

早就想写一个关于反卷积的总结，今天才得以动笔。

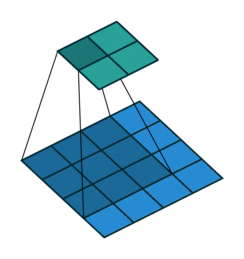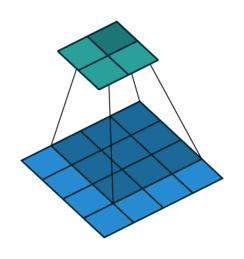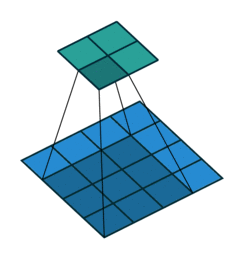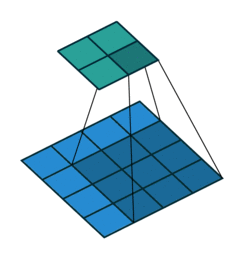
卷积-过程示意图

对于上述卷积运算，可以把3×3的卷积核展成如下4×16的稀疏矩阵C，其中非0元素Wij表示卷积核的第i行和第j列。

卷积核展开为矩阵

再把4×4的输入特征展开成16×1的矩阵X，那么Y=CX是一个4×1的输出特征矩阵，重新排列为2×2的输出特征就得到最终的结果。

从上面过程可以看出，卷积层的计算可以转化为矩阵相乘。

卷积层的前向操作可以表示为权值组成的矩阵C和输入特征Y相乘。

由于矩阵C一般没有逆矩阵C-1，但是可以用矩阵C的转置CT近似。

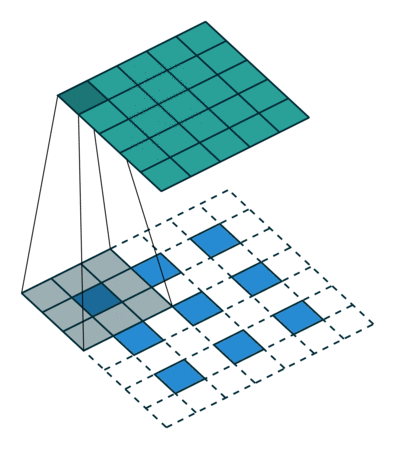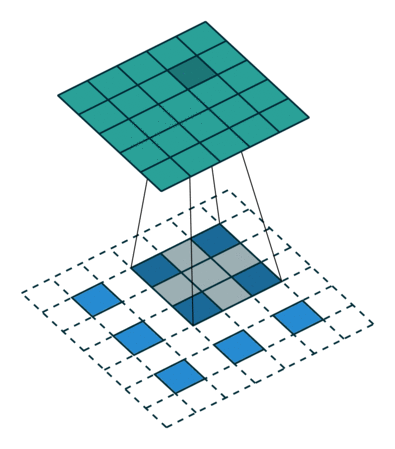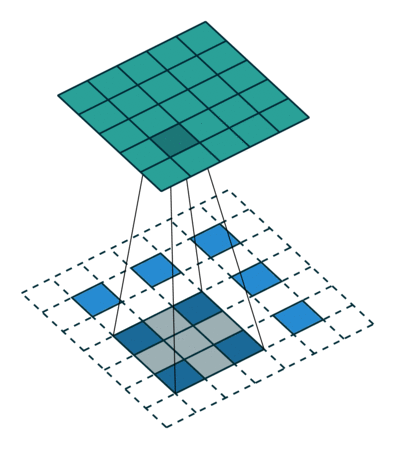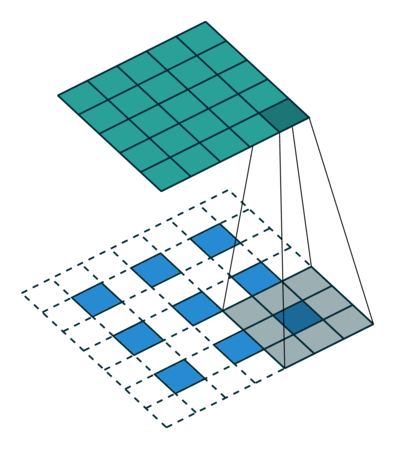
卷积-小数步长-过程示意图

在其输入特征单元之间插入s−1个0，插入0后将其作为新的输入特征。

此时步长不再是小数而是1。

以下均考虑S(步长)为1的情况。

S(步长)为1时，输出特征图比输入特征图小。

一般表现为卷积之前不补K-1//2个0。

Half padding，S(步长)为1时，输出特征图和输入特征图`大小相同。

有pool的时候经常需要Same卷积。

S(步长)为1时，输出特征图比输入特征图大。

一般表现为卷积之前补K-1个0。