偏差与方差
偏差:准确性,预测值的期望与真实值之间的差距。偏差越大越偏离真实数据。
方差:稳定性,预测值的离散程度。方差越大数据越分散。
目标:低偏差和低方差,也就是高准确性和高稳定性。
偏差-方差分解
“偏差-方差分解”试图对学习算法的“期望泛化错误率”进行拆解。
泛化误差 = 偏差 + 方差 + 噪声
具体解析:

“偏差”度量了学习算法的期望预测与真实结果的偏离程度,刻画了“学习算法本身的拟合能力”。
“方差”度量了训练集的变动所导致的学习性能的变化,刻画了“数据扰动所造成的影响”。
“噪声”表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,刻画了“学习问题本身的难度”。
“偏差-方差分解”说明,“泛化性能”是由“学习算法的能力”、“数据的充分性”以及“学习任务本身的难度”所共同决定的。
偏差-方差窘境
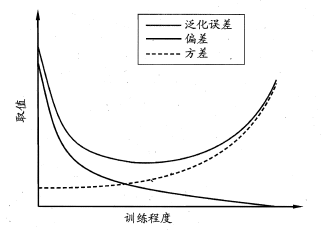
一般来说,偏差与方差是有冲突的。
给定一个学习任务,假定我们能控制学习算法的训练程度。
在训练不足时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器产生显著变化,此时“偏差”主导了泛化错误率。
随着训练程度的加深,学习器的拟合能力逐渐加强,训练数据发生的扰动渐渐能被学习到,“方差”逐渐主导了泛化错误率。
在训练程度充足后,学习器的拟合能力已非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特征被学习器学习到了,则将发生过拟合。
Reference
《机器学习 - 周志华》第2章 模型评估与选择
